4: Medicine + Technology + Art

The Hippocratic Oath
http://www.pbs.org/wgbh/nova/
body/hippocratic-oath-today.html

Before this week, I never really thought of practicing medicine as an art.  It just seemed incredibly science-based and precise.  At first, calling it an art made it seem like doctors kind of messed around and tried things in the hopes that they could heal patients.  But now, I understand a bit of why medicine can be called an art.  The process of treating a patient or performing a surgery can be very artistic.  In fact, the precision that makes medicine seem like science also makes it more like art.  When doctors work, it is like an artistic performance, carefully thought through and carried out. The Hippocratic Oath that doctors take shows the gravity of the work they do.

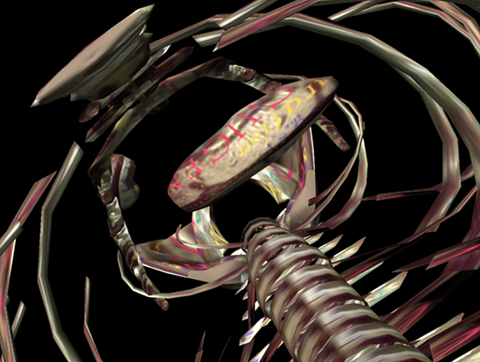Still from Digital Dervish, 1993
Diane Gromala and Yakov Sharir
http://gromala.iat.sfu.ca/New/dervish.html

Looking at art that uses medical technology, one thing that struck me was that for the most part, the artists use their own bodies in making their art.  Some of it actually involves having surgical procedures on themselves.  For example, Orlan went through plastic surgery in her artwork.  This type of art seems more personal and internal than other types because the artist’s body is so often used.  Diane Gromala does art and research using virtual reality and biofeedback.  She is interested in studying the internal senses of the body, so although she doesn’t change her own body for art, she is exploring something deeper inside.  The image on the right is from a virtual reality inside the body. Casini describes something similar in MRI, where her focus is not on the static images obtained, but the sounds and movements experienced.

The anatomy of the body has long been used in art; people have always been fascinated with the human body.  Of course, this is not surprising because the body is complex and beautiful.  In his article, Ingber explores the architecture of many biological structures that are similar.  Because of tensegrity, stress can be distributed across structures in unexpected ways and perform certain functions.  Different patterns in structures recur in many different organisms in nature.  It is amazing that living things are so distinct and unique yet also have so many similarities.

A model of part of a DNA string using tensegrity.  I think it's pretty cool.

http://www.tensegriteit.nl/e-dna.html

Sources:

Casini, Silvia. "Magnetic Resonance Imaging (MRI) as Mirror and Portrait: MRI Configurations between Science and the Arts." Configurations 19.1 (2011): 73-99. Web. 21 Apr. 2016.

Ingber, Donald E. "The Architecture of Life." Sci Am Scientific American 278.1 (1998): 48-57. Web. 21 Apr. 2016.

Medicine pt1. Youtube.com. Web. 21 Apr. 2016.

TEDxAmericanRiviera - Diane Gromala - Curative Powers of Wet, Raw Beauty. Youtube.com. Web. 21 Apr. 2016

Tyson, Peter. "The Hippocratic Oath Today." NOVA. PBS, 2001. Web. 21 Apr. 2016.

3: Robotics + Art

A robotics tournament at my high school. My idea of robotics.
http://thesmokesignal.org/2014/02/01/1100-am-1230pm
-live-coverage-of-msj-robotics-tournament/

When I think of robots, what usually first comes to mind are the contraptions built by school robotics teams.  It was interesting to learn from Professor Kusahara's lecture that in Japan, most robots are humanoid and are considered friendly.  It contrasts with the Western view of robots, which usually involves either an assembly line or robots taking over the world.  Our idea of robots came from industrialization, which actually originated from the printing press.  Industrialization is often associated with wars and the suffering of the lower class, so it is no wonder that we have a more negative or machine-like perspective of robots.

Japanese humanoid robots
http://www.newsweek.com/robot-reads-your-emotions-go-sale-japan-345167

The development of robots and industrialization affected art in that it allowed for mass production.  Walter Benjamin claimed that mass production endangered the originality of art because it could be more easily reproduced.  He also predicted that art would not be as appreciated and would be geared toward the masses.  This can be seen in mass media and entertainment today.  However, the reproducibility of art has also changed how art is created today.  Moving on from mass production, art can now be shared and reproduced virtually.  This has resulted in more collaboration and the blending of unique voices.  It has also created more outlets for creativity and made projects more accessible.  For example, Arduino is a platform that allows people with all sorts of interests to create whatever they wish.  Because it is open-source, users have access to a large amount of helpful knowledge.  Reproducibility of projects allows people to build on others' work.  With industrialization, art has changed from something very original and personal to something that is shared, but still is unique.

Arduino 101 board
http://www.arduino.cc/en/Main/ArduinoBoard101

Sources:

"Arduino - Introduction." Arduino - Introduction. Arduino. Web. 14 Apr. 2016.

Benjamin, Walter. The Work of Art in the Age of Mechanical Reproduction. 1936. Print.

Davis, Douglas. "The Work of Art in the Age of Digital Reproduction (An Evolving Thesis: 1991- 

1995)." Leonardo 28.5 (1995): 381-86. JSTOR. Web. 14 Apr. 2016.

"Relating the Rapidly Changing Present to the Distant Past as Far as Book History Is Concerned."  

HistoryofInformation.com. Jeremy Norman & Co., Inc. Web. 14 Apr. 2016.

Robotics MachikoKusahara 1." Youtube.com. Web. 14 Apr. 2016.

2: Math + Art

I never really appreciated mathematics until I took a calculus class.  It was then that I began to see how math could be cool and even pretty amazing.  So now, I can better understand why math is even used in art in the first place.  Math often deals with concepts that seem really mind-blowing or profound, like multiple dimensions and complex systems.  From my understanding, these concepts are deep enough that artists would want to use them or explore them.  For example, in Flatland, different dimensions are used to display the somewhat limited perspectives and worlds of the shapes.  The ideas explored in Flatland could potentially be applied to many different things, but using math creates something that is very easy to see and understand for most people.

An image from Flatland.  To a 2-D shape, a 3-D sphere that moves looks like a circle that changes size. http://www.geom.uiuc.edu/~banchoff/Flatland/

Painting by Piero della Francesca, who studied
the mathematics of perspective.

Math can also be really simple and model the ordinary things around us.  For example, in the lecture video we learned about how painters used math to control the perspective of a spectator.  It seems pretty simple to paint a realistic painting, but in actuality there is a lot of math involved to make it look so real in its proportions.

The Mandelbrot Set

As mentioned before, I didn’t really have any interest in math until recently. However, in high school I did look into chaos theory, which also involves looking at fractals, like the Mandelbrot set.  At the time, I thought fractals were really interesting because it was order within disorder, and they show up in nature everywhere.  I also thought they looked really cool, but I never thought of them as having to do with art because I was looking at them from the point of view of a physical scientist.  But it is no surprise that artists use fractals in their work.  I had no idea that Jackson Pollock used fractal patterns in his drip paintings.  I think it is fascinating that he used such complexity and tried to stick to fractal dimensions that were close to those in nature so that perhaps they would be more pleasing to the human eye (though I don’t think he had a way of measuring fractal dimensions).  

Blue Poles, by Jackson Pollock
http://www.jackson-pollock.org/

From this week and the last, I’ve been exposed to more art that uses math and science, but still not really any science or math that uses art. So I would say that the juxtaposition of mathematics, art, and science is somehow one-sided.

Sources:

Abbott, Edwin. Flatland. 1884. Web. 09 Apr. 2016.

Flatland: A Romance of Many Dimensions. By Edwin Abbott. 1884. Transcript.

Ouellette, Jennifer. "Pollock's Fractals." Discover Magazine. Kalmbach Publishing Co., 1 Nov. 2001. Web. 09 Apr. 2016.

Vesna, Victoria. "Mathematics-pt1-ZeroPerspectiveGoldenMean.mov." Youtube.com. Web. 9 Apr. 2016.

Weisstein, Eric W. "Mandelbrot Set." Wolfram MathWorld. Wolfram Research, Inc. Web. 09 Apr. 2016.